B 树(B- 树)是 MySQL 最常用的索引数据结构。B 树常用于大数据量的场景中,是 MySQL 索引实现的核心,大厂校招、社招面试 90% 会问到。
引入 B 树 ,是为了解决高频的 I/O 操作。在操作系统中,I/O 的成本是很高的。
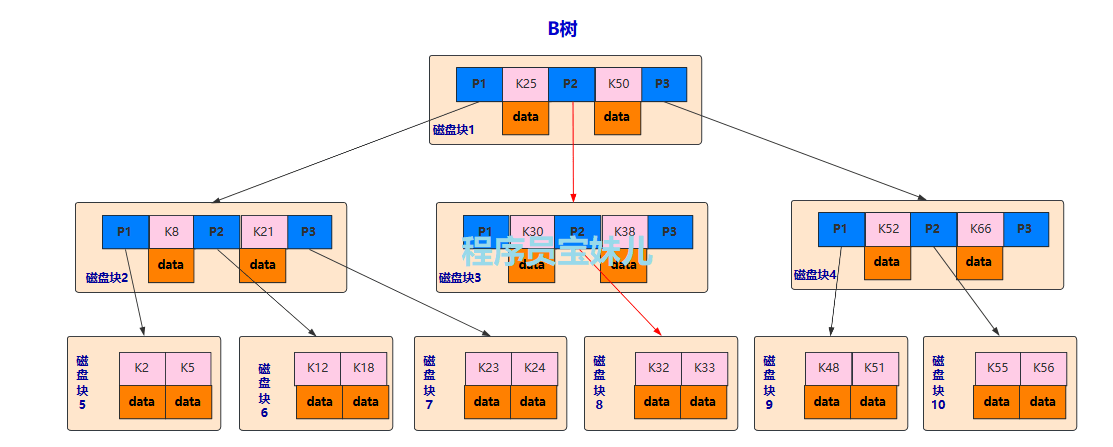
B 树的每个节点存储的数据量约为 4K。磁盘数据存储是采用块的形式存储的,每个块也是 4K。
每次对磁盘进行 IO 数据读取时,同一个磁盘块的数据,就会被一次性读取出来。每一次磁盘 IO ,都可以读取到 B 树中一个节点的全部数据。从而避免了高频的 I/O 操作。
每层的节点数增加了,树高也随之减少,极大减少了 I/O 次数。读取一个节点时,就可以一次性读取大量关键字数据。
本文我们详解 B 树:
- 树的基本概述
- B 树的概念
- B 树的结构
- B 树的特性
- M 阶 B 树
- B 树的插入
- B 树的删除
- B 树与平衡二叉树的区别
PS.
大家好,我是爱分享的程序员宝妹儿,分享即成长。
索引基础也是面试考察重点,在回答基础题时,如果你能加入一些自己的理解,也会是加分项。
宝妹儿已将本文更新到《MySQL 大厂高频面试题大全》PDF了,方便系统学习、面试通关。
《MySQL 大厂高频面试题大全》PDF,已收录100+道真题,一共78页,近50000字,文末自取。
吃透它,足以应付MySQL面试。

1. 树的基本概述
B 树是树的类型之一,先来温习树的基础知识,这样可以更好地理解并掌握 B 树。
树是一种数据结构,由于其结构像一棵树,因此取名“树”。
树由有限个节点组成具有层次关系的集合,包含了 n 个节点(n 为大于 0 的整数),n-1 条边的有穷集。
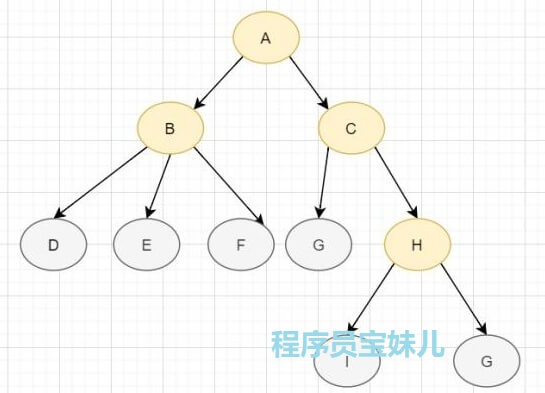
一颗普通树的结构:
树的常用术语:

树的特点:
- 每个节点要么无子节点,要么只有有限个子节点;
- 存在一个特殊节点作为树的顶部,没有父节点,称为根节点;
- 每个非根节点、只有一个父节点,形成层次结构;
- 树中不存在环路。
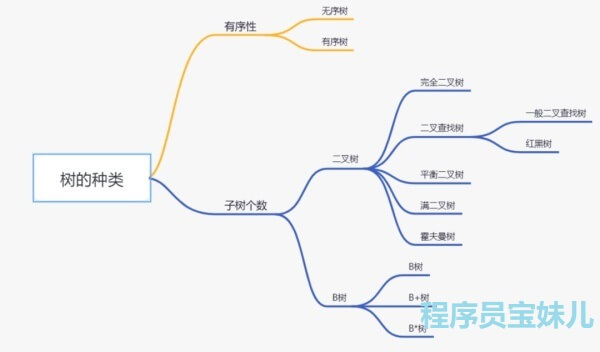
树的类型:
按照树的有序性,分为有序树、无序树。
按照树的节点所包含的子树个数,分为 B 树、二叉树。
二叉树又可以分为二叉查找树、满二叉树、完全二叉树、霍夫曼树、红黑树、平衡二叉树(AVL)。
2. B 树的概念
B 树是一种平衡多路查找树,又称为 B- 树、平衡查找树。
注意:B 树和 B- 树是同一种树。
B 树的自平衡树状数据结构,让它能够对存储的数据进行 O (log n) 的时间复杂度的查找、插入和删除。
因此,B 树适用于对外查找,通常用于存储系统,例如数据库、文件系统等。
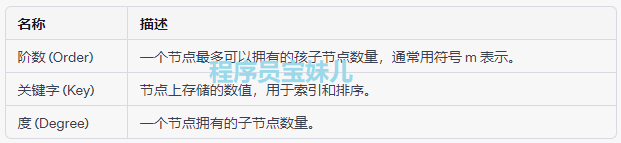
B 树的常用术语:
3. B 树的结构

- P:指针,即存储子节点的地址
- K:键值,即表中记录的主键
- data:数据,即除主键之外的数据
这里解释下:
1)每个节点占据一个磁盘,一个节点上有:
- 两个升序排序的关键字 K ;
- 三个指向子树节点的指针 P ;
- 指针 P 存储子节点所在磁盘块的地址 。
2)两个关键字 K 划分成三个范围域,对应整个指针指向子树的数据范围。
以根节点(所在磁盘块 1 )为例:
- 关键字为 25 和 50 ;
- P1 指向数据范围小于 25 的子树 ;
- P2 指向数据范围在 25 和 50 之间的子树 ;
- P3 指向数据范围大于 50 的子树 。
4. B 树的优缺点
B 树的优点
大数据量的场景中,B 树在高效存储和检索方面很具有优势,特别是在磁盘随机存取的环境下。
- B 树始终保持平衡,操作的时间复杂度可保持在 O(log n) 级别;
- 减少树的层数,降低了在磁盘等存储设备上的访问次数,提高了数据访问效率;
- 每个节点内关键字有序,适用于范围查询和顺序遍历等操作;
- 能够自动维护平衡性,适用于动态数据更新场景。
B 树的缺点
但是,B 树的实现和维护相对复杂,可能会增加空间开销、影响性能。
- 实现相对复杂,需要处理节点分裂、合并等操作,增加了代码复杂性。
- 节点存储多个关键字和子节点指针,如果存储数量很大,会导致深度较大,增加了查询时磁盘 I/O 的次数,影响性能。
5. B 树的特性
一棵普通 B 树:

5.1 B 树的规则
- 任意非叶子节点:最多只有 M 个儿子(M>2);
- 根节点的儿子数:为 [2, M] ;
- 除根节点以外的,非叶子节点的子节子数:为 [M/2, M];
- 每个节点存放最少 M/2-1 (向上取整)、以及最多 M-1 个关键字 (最少 2 个关键字);
- 非叶子节点的关键字个数 = 指向子节点的指针个数 – 1;
- 非叶子节点的关键字: K[1], K[2], … ,K[M-1],并且 K[i] < K[i+1];
- 非叶子节点的指针: P[1], P[2], ….,P[M]。其中,P[1] 指向关键字小于 K[1] 的子树,P[M] 指向关键字大于 K[M-1] 的子树,其它 P[i] 指向关键字属于 (K[i-1], K[i]) 的子树;
- 叶子节点的层次:所有叶子节点位于同一层。
5.2 B 树的特点
- 叶子节点具有相同的深度,叶子节点的指针为空;
- 节点中的数据从左到右递增;
- 关键字分布在整个树中,每个关键字在树中只出现一次;
- 搜索可能在非叶子节点结束,而不仅仅限于叶子节点;
- 搜索性能等同于在关键字全集内执行一次二分查找;
- 树的层次自动调整,不会因数据分布而过于倾斜;
- 当 B- 树作为索引元素时,所有的索引元素不可以重复。
6. M 阶 B 树
一棵 3 阶 B 树:
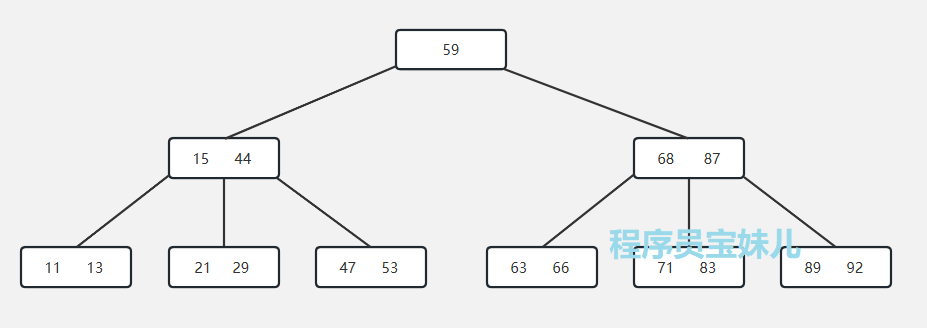
一棵 m 阶 B 树的特点
1) 根节点
- 如果不是叶子节点,包含 k-1 个元素和 k 个孩子 。其中, 2 <= k <= m。
- 如果是叶子节点,元素数量没有下限,上限为m-1。
2)中间节点
包含 k-1 个元素、k 个孩子,其中,[m/2] <= k <= m。
3)叶子节点
包含 k-1 个元素,其中,[m/2] <= k <= m)。
4)所有的叶子节点位于同一层
5)每个节点的元素从小到大排列
节点当中 k-1 个元素,正好是 k 个叶子节点包含的元素的值域的分隔值。
注意:[m/2] 向上取整,例如 [4/2]=2, [5/2]=3
7. B 树的插入
B 树的插入操作,主要是为了保持 B 树的平衡性和有序性,让 B 树仍然能够高效地支持查找、动态数据插入和维护的场景。
哪些情况下,我们需要 B 树插入操作呢?
1)叶子节点未满
当插入的关键字所在叶子节点的关键字数量、未达到节点的上限时,直接插入关键字,保持有序性。
假设 B 树的阶数为 3 。
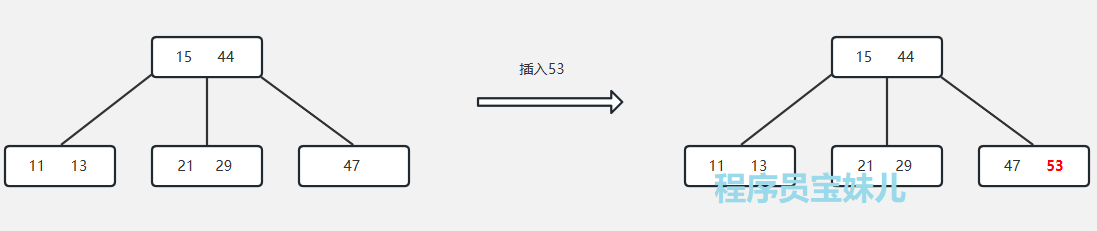
当叶子节点中的元素数量小于最大值时,可直接插入关键字 53 ,以保持 B 树的有序性。
2)叶子节点已满
- 如父节点未满: 插入关键字导致叶子节点的关键字数量超过了上限,但其父节点还有空间,可以进行分裂操作,将关键字插入叶子节点并进行必要的调整。
- 如父节点已满: 插入操作可能导致父节点关键字数量超过上限,此时就需要递归向上分裂父节点,保持整个 B 树的平衡性。
假设 B 树的阶数为 3 。

解析下:
- 在这个节点中的元素、以及新添加的元素中,找到中位数;
- 将这个节点分裂成为 2 个节点;
- 将小于中位数的元素,放到左边的节点;
- 将大于中位数的元素,放到右边的节点;
- 将中位数作为分隔值,插入到父节点中。将中位数插入到父节点中,可能会导致父节点分裂,以此类推;
- 如果没有父节点(根节点) , 就创建一个新的根节点。
分裂节点后,2 个节点的元素数量,是否满足了 B 树的特性(平衡性和有序性)?
一个节点最少需要 ⌈m/2⌉-1 个元素。
两个节点需要的元素数量为 2 *(⌈m/2⌉-1):
- m 为偶数时,2* (⌈m/2⌉- 1)= 2*(m/2- 1) = m-2
- m 为奇数时,2* (⌈m/2⌉- 1)=2* ((m+1)/2- 1)= m-1
而当前节点除了中位数,剩下的元素数量为 m-1,大于等于上述两个计算值,足够分裂为两个节点,已满足 B 树的特性。
8. B 树的删除
B 树的删除有两种情况。
假设:删除的元素为 D
第 1 种情况:D 是叶子节点上的元素。
第 2 种情况:D 是非叶子节点上的元素。
第 2 种情况可以转化为第 1 种情况,只需要用 D 左子树的最大元素、或右子树的最小元素替换掉 D,再移除这个最小元素 。
此时,这个最小元素是在叶子节点上的。这两种情况,就转化成了一种情况。
将 D 直接从叶子节点中删除,该叶子节点中元素的数量,仍然满足 B 树的性质。如果该叶子节点是根节点,删除 D 后,它仍然满足 B 树性质,就不会再往下走了。
因此,叶子节点肯定不是根节点,它必然有父节点,并且父节点最少有一个元素。

按照 B 树的性质(叶子节点数量=元素数量+1),父节点最少有 2 个叶子节点,那么,该叶子节点一定存在兄弟节点。
该叶子节点中,元素的数量是最小数量,在删除 D 后,不能满足 B 树性质了。
此时,就需要进行调整:
1)如果该节点的右兄弟存在,并且拥有多余的元素:
将父节点的分隔值移到该节点的最后,用右兄弟的第一 个元素替换掉父节点的分隔值,树又重新平衡了。

2)如果该节点的左兄弟存在且拥有多余的元素:
将父节点的分隔值移到该节点的第一个元素,用左兄弟的最后一个元素替换掉父节点的分隔值, 树又重新平衡了。

3)如果该节点的两个直接兄弟节点,都只有最小数量的元素:
将它的一个直接兄弟与父节点的分隔值、以及 D 合并为一个节点。
将父节点的分隔值,移到左边的节点。
将右边节点中所有的元素,也移到左边的节点(右边节点空了),将空的右子树移除。
4)如果父节点元素数量不满足,重新平衡:
如果父节点是根节点,则删除原来的根节点,并且将合并后的节点作为根节点。

那么,合并后的节点,是否满足 B 树的性质呢?
删除 D 后,该叶子节点的元素数量为 ⌈m/2⌉ – 2,它的直接兄弟节点的元素数量为⌈m/2⌉- 1,再加上父节点的分隔值,合并后的元素数量为:
(⌈m/2⌉-2)+ (⌈m/2⌉-1)+ 1 = 2*⌈m/2⌉ -2
- 当 m 为偶数时,2*⌈m/2⌉-2 = m-2
- 当 m 为奇数时,2*⌈m/2⌉-2= 2*⌈(m+1)/2⌉-2= m-1
按照 B 树的性质,节点最多有 m-1 个元素。
上述计算出来的值,都小于、等于 m-1,因此满足 B 树的性质。
9. B 树和平衡二叉树的区别
- 平衡二叉树的每个节点存储的数据很少,每次节点比较,都需进行 I/O 获取节点数据。二叉树在搜索时,需要大量的 I/O 次数,对 MySQL 的性能影响很大。
- B 树属于多叉树,又名平衡多路查找树(查找路径不止两个),B 树在节点空间的利用率上进行了改进。B 树的每个节点存储的数据量约为 4K。磁盘数据存储是采用块的形式存储的,每个块也是 4K。每次对磁盘进行 IO 数据读取时,同一个磁盘块的数据,就会被一次性读取出来。每一次磁盘 IO ,都可以读取到 B 树中一个节点的全部数据,从而避免了高频的 I/O 操作。
总结
通过本文,我们了解并掌握了 B 树的概念、结构、特性、原理,以及查询、插入、删除等操作。
B 树是一个节点可以拥有多于 2 个子节点的二叉查找树。数据库索引技术大量使用了 B 树的数据结构。
数据库索引技术大量使用了 B 树的数据结构。在大数据量场景中、磁盘随机存取的环境下,B 树在高效存储和检索方面很具有优势。
建议收藏备用,划走就找不到啦。
我是爱分享的程序员宝妹儿,分享即学习。
谢谢您的关注、点赞、建议。
PS.
本文已归录到宝妹儿精编的2023版《MySQL面试题大全》PDF,方便系统学习、面试通关。

